The Triangle Alphamill
A system of 10 concentric colourful triangles, spinning in both directions while their rotation values affect their transparency. Inspired by Morley's trisector theorem and generative geometric patterns.
produced by: Petros Veloussis
Idea & Structure
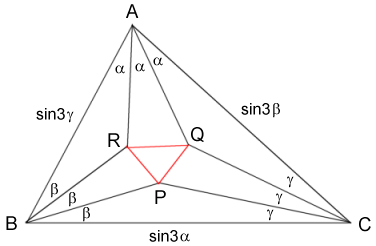
The idea for this program came up while reading about Morley's triangles and the trisector theorem, as well as my interest in geometric shapes and patterns. It consists of 10 spinning concentric triangles of different colors and dynamically varying alpha values. These triangles are divided in 3 groups, regarding their size and rotation speed.
In the first group we have a pair of the smallest and fastest spinning triangles. In the second one, 2 triads of medium size triangles spinning in medium speed, with their smallest sides(bases) facing each others' and thus, each triad can also be regarded as a single piece of three. Finally, in the third one, we have the two biggest in size and slowest in rotation triangles. Additionally, there are also two layers of them, splitting each group into half, with each layer having opposite(+/-) rotation angles. This means that the first layer consists of one small and one big triangle, plus a triad, that rotates clockwise, while the equal in size second layer, rotates counter-clockwise.
The program
To transfer the above mentioned "architecture" into the program, I am using a class where my triangle objects are constructed and 3 functions. Two of them correspond to the above mentioned 2 layers, which will display a 5 triangle "system" each. The difference between "displayLayerA" & "displayLayerB" functions, is in the way that alpha values are generated and mapped to sin and cos respectively.The third function of the class, "spin", will rotate the objects according to the "deltaTheta's" positive or negative values. Although the rotate function is placed in the 2 display functions, by calling the "spin" function in the main tab and setting a float number of "deltaTheta" in the parentheses, it will pass that number to theta and thus, the rotating mechanism will be activated, as welll as the influencing of the alpha values.
In the main tab, three "scene" functions are created according to the three triangle groups. Following some timing conditionals, the three, different in size and rotation speed, groups, will appear on screen one after the other, until all of them are added, going from the smallest to the biggest. On the program start, some seconds have intentionally been left without any action. In each one of the three scenes, the Triangle class functions are called to display ("displayLayerA" & "displayLayerB") and rotate ("spin") the triangles. Finally, a mouse click interaction was added, to switch between updating and non updating background color (draw & setup), to create a spirograph like effect.
Conclusion
I found the result of the program very interesting, as I think it has multidimensional aspects, regarding the geometric patterns, the linearity of the different groups and layers presentation, as well as the time dimension. Finally, the colors and moreover the dynamic alpha values, which make the triangles move on top of each other over time. Through their fading in and out transparencies, they seem to break the rules of the already structured groups and layers, thus, creating a 3D illusion sporadically. In addition, it gives viewer the illusion that triangles change rotation direction as they spin. By combining computational and human set aspects, this work produces an overall result, that I think, brings simplicity and complexity together, while being eye catching.
References
https://en.wikipedia.org/wiki/Morley%27s_trisector_theorem