An Experimental Prototype of Rhythm Generator
A practice-based research project that aimed to develop a working prototype to reflect my experiment with rhythm generation in the context of algorithmic composition, live-coding, and human-computer interaction.
produced by: Adam He
The working prototype
Introduction
In my algorithmic composition practice, I feel the needs of developing my gears for generating musical materials, because existing tools cannot solve some of the problems I am facing. There are serval issues I tried to address in this project, and they are of rhythm generation, toolkit modularity, intuitive interface, and live-coding syntax. I studied some modern theories on musical rhythms, investigated the algorithms used to generate these rhythms, and developed a working prototype that produces control signal sent to external devices to realise a specific type of rhythms. The prototype was designed to be a portable module adaptive to the graphics-based programming environment of Max/MSP, and at the same time takes advantage of the text-based programming modality that is essential for live-coding. I also invented a concise syntax for commanding the rhythm generation.
Context
There is music without tones, but there is no music without rhythms. While rhythm is such an indispensable foundation of music, in the Western music tradition, there have been relatively fewer theories about rhythm than other aspects, such as pitch and scale, of music. Modern researchers in the field have shown more interest in studying rhythm. Euclidean rhythm theory (Toussaint 2005) is one of the important rhythm theories developed in recent years and has been used for musical analysis and composition by researchers and musicians. Using this theory, Osborn (2014) analysed in a journal article the rhythmic structure of some of the works by Radiohead, in which Euclidean rhythm can be found extensively, despite the fact that some of those works were made before the theory had been formulated. Another notable analytical method is transformed from the well-formed scale theory (Carey and Clampitt, 1989) by Milne and Dean (2016). Well-formed rhythms are a superset of Euclidean rhythms, as such, they share the same underlying principle of maximum evenness, which I will describe later in the article.
On top of that, in the field of algorithmic composition, there are tools that incorporate these theories into their functions for rhythm generation. For instance, two of the well-known musical programming languages, SuperCollider and TidalCycles, all have built-in functions generating Euclidean rhythms. Also, there is also an application, XronoMorph (Milne et al., 2016), can produce well-formed rhythms. However, while the rhythm generation functions of these languages or applications are well-developed, there are still many reasons for music makers not to choose them as their tools. One of which would be because these tools are rather task-specific, meaning neither are they designed to be suitable for a musician to finish a piece of music entirely or almost entirely on the platforms they are built into, nor are they easy to be integrated into other existing programming environments. For example, there is no comfortable way to put the sophisticated sequencing functions of TidalCycles into the clip-based architecture of Ableton Live, and, XronoMorph runs more like an educational tool for discovering and studying rhythms rather than a productivity gear that can adapt to existing music-making workflows.
By contrast, with respect to cross-platform integration, Max/MSP has been doing well in recent years. This programming language is characterised by its intuitive graphic interface favoured by artists who know little about text-based programming, and its well-designed integration with Ableton Live and Javascript makes it even more popular. With Max/MSP, one can easily build their own tools in a modular manner. This gives artists and musicians the necessary flexibility in terms of adapting to the non-linear nature of artistic creation. Yet, Max/MSP does not have a function that is able to produce rhythm directly using Euclidean or well-formed theory. Apart from that, while dominating many procedural music-making scenarios with its user-friendly features, Max/MSP has always been excluded from the text-based live-coding toolsets because of it is graphics-based in the first place.
Objective
Therefore, in my algorithmic composition practice, after having tried working with different software environments, a question arose. That is, how to make a tool for generating rhythms that incorporates modern rhythm theories, and has an intuitive user interface working in a modular manner adaptive to flexible environments, and also, takes advantage of the text-based programming modality that is essential in live-coding scenarios. In this project, I aimed to develop a working prototype to reflect my experiment for the above question.
Related Rhythm Theories
To start the project, I studied the principle of maximum evenness. As Toussaint (2005) pointed out, the common characteristic that exists across African rhythms, spallation neutron source accelerators in nuclear physics, string theory in computer science, and an algorithm devised by the ancient mathematician Euclid, is the maximum evenness in the distribution of patterns. Specifically, in the context of music, interesting rhythms are often related to evenly distributed onsets under given metric constraints (Toussaint, 2013). For example, given the metric setting with sixteen evenly distributed inaudible pulses per periodic cycle, and we notate the duration between any two consecutive pulses as 1, if there are five audible onsets being put into this metric structure, the rhythm is likely to be more interesting if the set of intervals between the onsets is something like 3-3-3-3-4 rather than 1-2-3-4-6, because the former has more evenness than the latter. But of course, this excludes cases such as 4-4-4-4 where it is actually quite boring because there is no variation at all. In fact, an important rule of thumb for musical composition is to find the balance between variation and consistency. Maximising evenness under musical constraints that prevent perfect evenness, therefore, usually fits this principle.
For maximising evenness, there are two types of rhythmic arrangements that can meet the criteria. One is of Euclidean rhythms, and the other is of well-formed rhythms. By definition, the former needs to conform to a grid-based metric structure, just as the above-mentioned example of maximum evenness in a fixed metric setting. One of the notation conventions for representing a Euclidean rhythm looks like 3-2-3-2-3 (for five onsets arranged in a thirteen-pulse periodic pattern). In contrast to Euclidean, a well-formed rhythm (Milne and Dean, 2016) does not have this constraint, so it allows for subtle deviations from the grid which could result in interesting musical tension. Instead, it requires the onset intervals to have no more than two lengths. Typically, the two lengths are notated as l and s, respectively for long length and short length, so that a well-formed rhythm can be described as something like l-s-l-s-l. Here it is evident that the Euclidean rhythm 3-2-3-2-3 can be represented as a well-formed rhythm l-s-l-s-l, where l and s are not required to be integers because there is no fixed grid-based structure for well-formed rhythms. Thus, well-formed rhythms are a superset of Euclidean rhythms, meaning all Euclidean rhythms are well-formed, but not vice versa. Additionally, well-formed rhythms can be constructed hierarchically producing complex poly-rhythms, this will be described in detail later with the study of the respective application.
Application Study
While Euclidean rhythms can be created by many software programmes such as SuperCollider and TidalCycles, for well-formed rhythms, to the best of my knowledge, so far there is only one application, XronoMorph (Milne et al., 2016), can generate them. For better understanding the usage, I studied the applications.
First of all, SuperCollider, TidalCycles are text-based programming languages, and they conduct generating Euclidean rhythms with similar syntax. In TidalCycles, an example snippet of the syntax is “euclid 3 8”, here the 3 defines the number of onsets in the rhythmic pattern, and the 8 dictates the pattern to have eight pulses. As for SuperCollider, Euclidean rhythms are realised by an external library Bjorklund quark, whose function example is like “Pbjorklund2 (3, 8)” delivering the same action. It also needs to be remarked that the common algorithm used in generating Euclidean rhythms both in TidalCycles and SuperCollider is devised by Bjorklund (2003) initially for an application in nuclear physics.
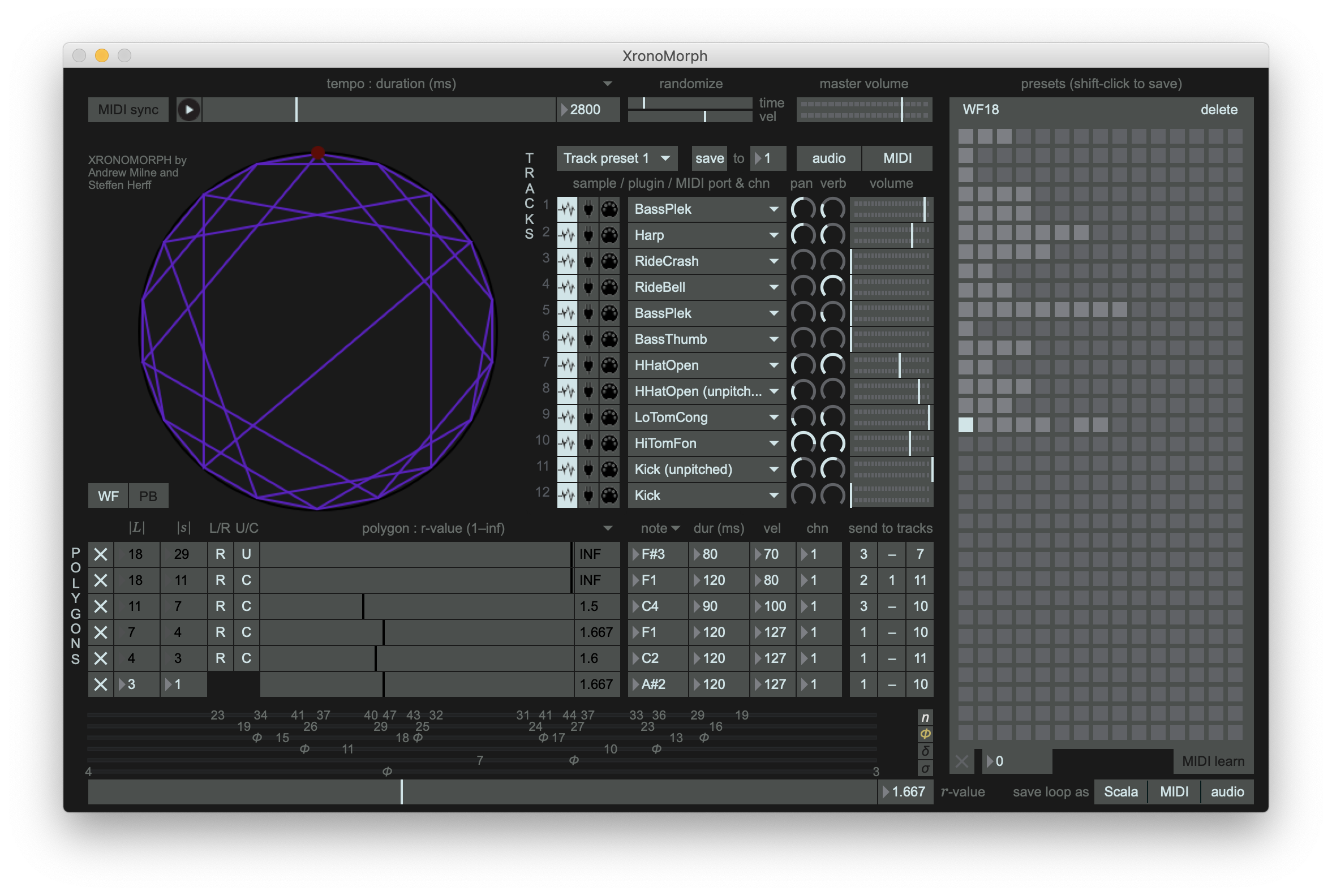
In contrast to those two text-based applications, XronoMorph uses an intuitive graphic interface with a circle representing the periodic cycle of a rhythmic pattern, aligning with the circle are the dots representing the onsets, which are grouped together forming polygons according to the layers they belong. The software has two modes of rhythm generation, which are Perfect Balance (PB) mode and Well-Formed (WF) mode. The two modes all aim to produce poly-rhythms through controlling the interval evenness. In PB mode, different layers of sound elements like bass drums, snares or hi-hats are arranged evenly along the pattern as shown as equilateral polygons aligning with the circle. There are multiple control components for entering the arguments of PB rhythms, such as the number of pulses of a pattern, the numbers and the timing offsets of onsets of each layer.
The user interface of XronoMorph
In WF mode, the polygons are no longer necessary to be equilateral, because in well-formed rhythms, the onset intervals have different lengths. More specifically, each layer of onset intervals have two lengths and are arranged following the principle of maximum evenness. The ratio between the longer intervals and the shorter ones can be set through a slider at the bottom of the interface. But what makes WF mode really powerful is its hierarchical structure of rhythm layering. There are six onset layers pre-built in WF mode, a higher layer is derived from the lower layer of one level down, so that means the lowest layer actually determines all the upper layers. The essential arguments for the bottom layer are the numbers of the long interval and the short one, which subsequently decide the numbers of long and short intervals of all the upper layers given a certain length ratio between the two set by the user. Additionally, the onsets of a layer can be optionally disabled if they overlap with the onsets of the lower layers, this handy function can avoid congestion in sound layering.
In practice, I found that using XronoMorph in WF mode can generate more interesting results compared with using SuperCollider, TidalCycles and the PB mode. This makes sense because well-formed rhythms cover Euclidean rhythms as previously described, in WF mode the application can produce higher rhythmic complexity. As such, I decided to use XronoMorph in WF mode as a reference for designing my prototype. However, as set to be one of the objectives of the project, the text-based modality of live-coding is to be employed, hence the next question is how to invent a syntax for representing the arguments in the WF mode. Moreover, the interface should also be minimal for being able to be used in a modular manner, that means it should only include the essential elements for generating well-formed rhythms, to the opposite of the interface of XronoMorph.
Prototype in Action
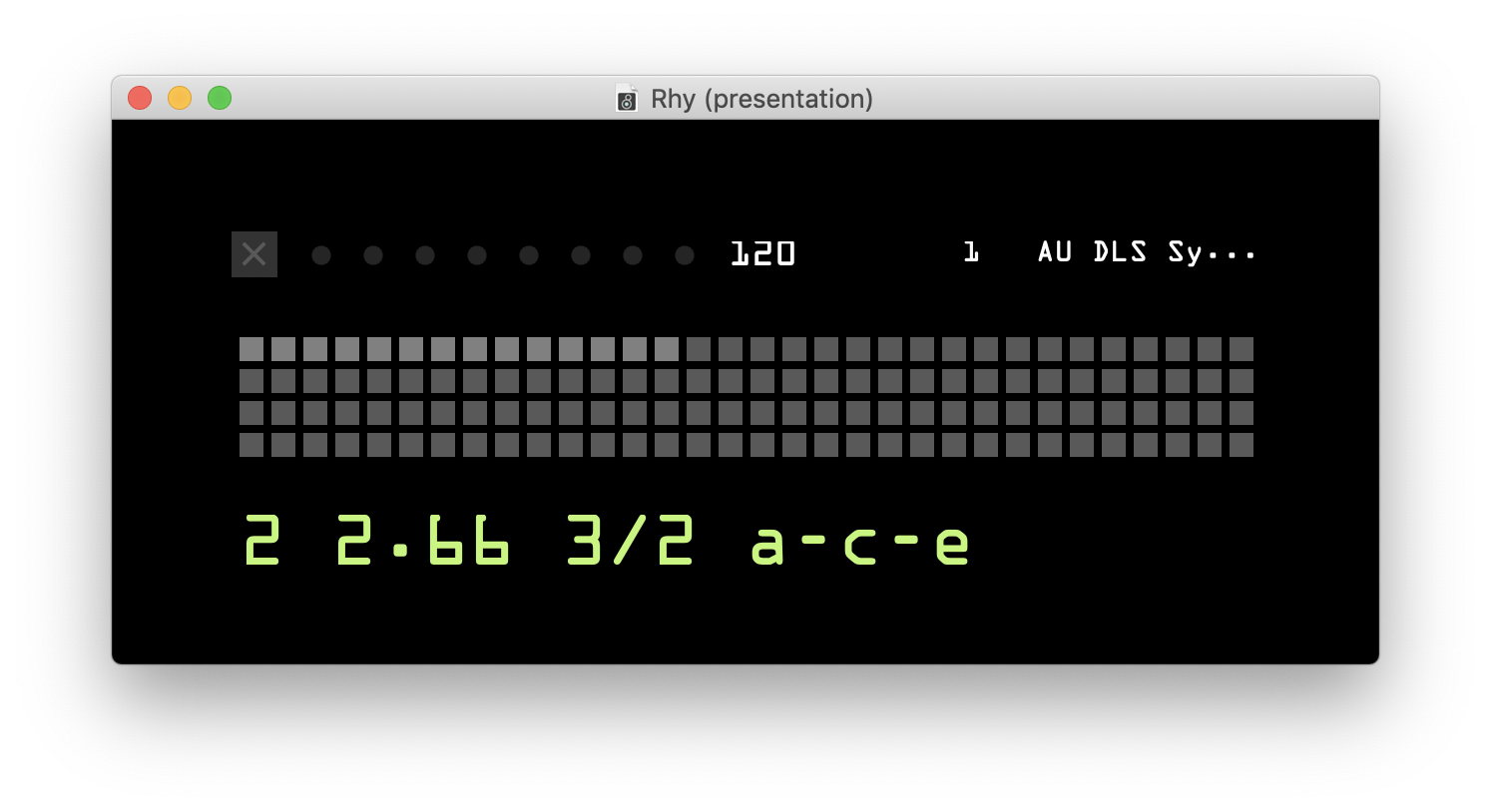
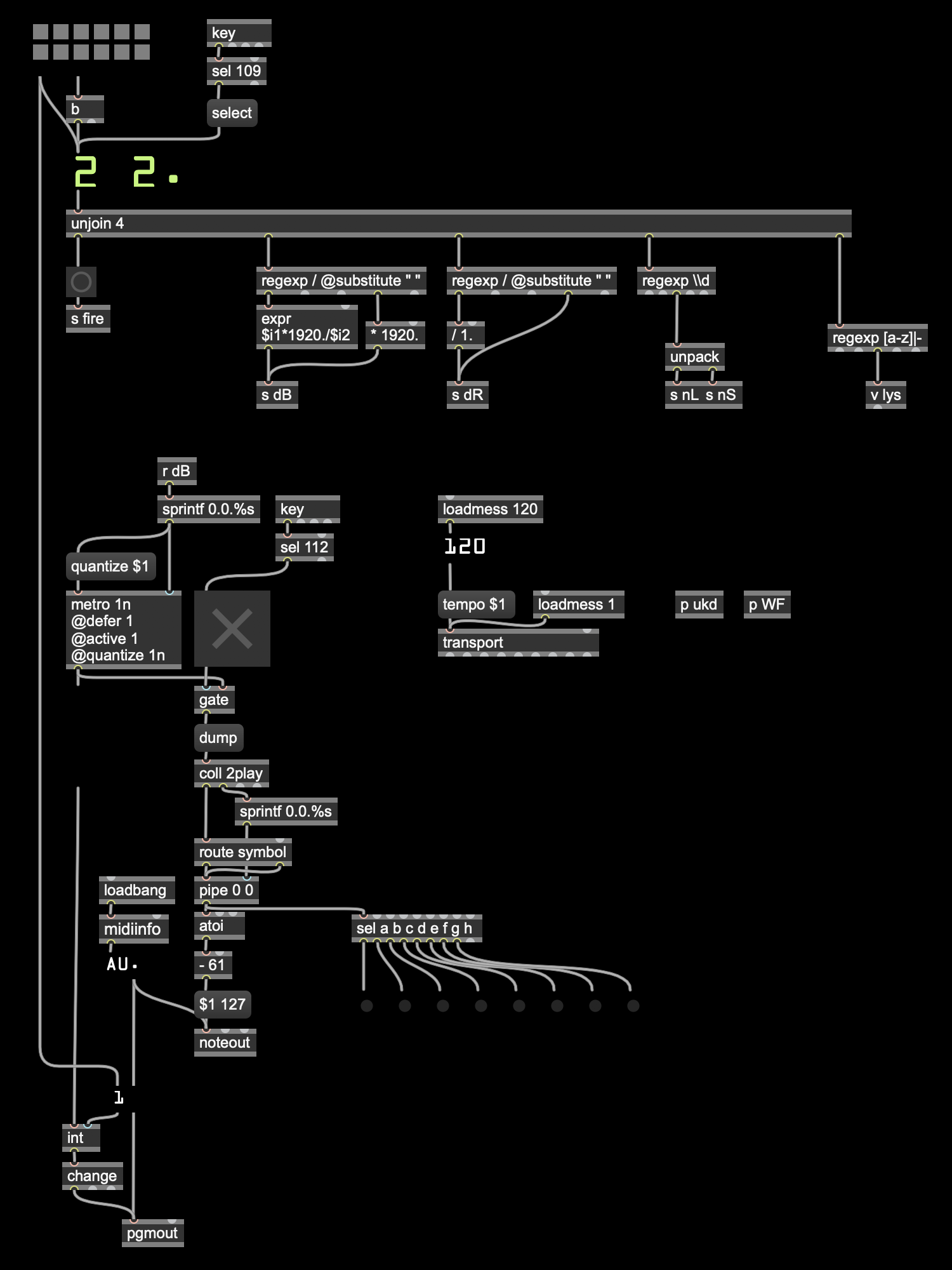
The prototype comes with a small size interface for the purpose of portability. In fact, it could be made even smaller by scaling down all the elements, but for the demonstration I had it larger than it is needed for real tasks. The most prominent component in the interface is the text editor for entering the arguments of a well-formed rhythm to be produced. These arguments, from left to right in the order of text command, are described as follows: First, it is a number deciding the overall duration of the pattern to be made. It can be an integer, a decimal or a fraction, the exact duration is calculated by multiplying this number to the length of a whole note or four beats, in relation to the beats per minute (BPM) set in the other component in the upper part of the interface. The second argument, is the ratio of the long onset intervals to the short counterparts, which can also be an integer, a decimal or a fraction. The third is a pair of integers, which are the number of the long onset intervals and the short ones. They are visually grouped by a “/” symbol for improving readability. The last argument is a letter string, of which each letter represents a sound element assigned to each layer of the poly-rhythm. For example, “a” can be mapped to a bass drum sound provided by an external device, and “b” for snare drum, and so on. The mapping can be arbitrary but a special usage of letter “-” for no sound. From left to right in the string, the letters are set for layers from the lowest to the highest respectively. With this syntax, one can effectively define the rhythm to be generated, exploiting the straight-forwardness of text-based programming.
Besides featuring the terse syntax, this small application also takes care of some other concerns. Firstly, it can to be used as a module inserted into the existing workflow of music-making. When in action, it continuously sends out MIDI notes to external devices including other modules in Max/MSP or applications in other environments such as Ableton Live or hardware synthesisers. Secondly, live performance scenarios are taken into account. By storing and recalling the text commands using the preset panel, one can switch between different pre-defined rhythms very quickly during the performance. What’s more, the helpful timing quantisation is coded into the behaviour, also, eight minimal virtual LEDs indicate in real time the triggering of the onsets. These functions actually are the complementary enhancements added on top of the purely text-based live-coding approach.
The user interface of the prototype
Evaluation and Further Development
Although being a prototype far from a full-fledged software, this mini-application can effectively use just one line of code to generate rhythms, whose complexity is greater than those yield by simpler Euclidean algorithms employed in the benchmark languages SuperCollider and TidalCycles, and is in some way comparable with those produced by more well-developed softwares, but with simpler workflow. After testing, the syntax has been proven to be clear and efficient, which could be a starting point of my future exploration of inventing a new live-coding language whose syntax is one of the main aspects of human-computer interaction (HCI). As a prototype it is focused on generating one type of rhythms, whereas for further development, there is nothing can stop it from using more algorithms producing other types of rhythms. Plus, it is designed to act as a portable module adapting to different software environments. In action, it works well controlling external devices. However, it could be further developed to be more adaptive. Some ideas include developing a version of Max for Live device which is integrated perfectly into the Ableton Live environment, or, an Open Sound Control (OSC) mode could be added on top on the current MIDI mode for communicating with more types of external systems. Furthermore, it demonstrates the merit of a graphics-text-hybrid interface, combining the advantages of both sides, affording an intuitive, straight-forward, and responsive approach for manipulating rhythms in real time. This aspect of exploration can go further by adding to it more text functions and keyboard shortcuts. Overall, this experiment results in informative inspiration, not only for rhythm generation, but also for my future exploration of algorithmic composition in a broader context with concerns about flexibility and usability of tools.
The developer interface of the prototype
References
Bjorklund. E. (2003) ‘A metric for measuring the evenness of timing system rep-rate patterns’, SNS ASD Technical Note SNS-NOTE-CNTRL-100. Los Alamos National Laboratory, Los Alamos, U.S.A.
Bjorklund. E. (2003) ‘The theory of rep-rate pattern generation in the SNS timing system’, SNS ASD Technical Note SNS-NOTE-CNTRL-99. Los Alamos National Laboratory, Los Alamos, U.S.A.
Carey, N. and Clampitt, D. (1989) ‘Aspects of Well-Formed Scales’, Music Theory Spectrum, 11(2), p. 187-206.
Milne, A. J. and Dean, R. T. (2016) ‘Computational Creation and Morphing of Multilevel Rhythms by Control of Evenness’, Computer Music Journal, 40(1), p. 35-53. doi: 10.1162/COMJ_a_00343.
Milne, A. J. et al. (2016) ‘XronoMorph: Algorithmic Generation of Perfectly Balanced and Well-Formed Rhythms’, 16th International Conference on New Interfaces for Musical Expression. Brisban, Australia, 11-15 July.
Osborn, B. (2014) ‘Kid Algebra: Radiohead’s Euclidean and Maximally Even Rhythms’, Perspectives of New Music, 52(1), p. 81-105. doi: 10.7757/persnewmusi.52.1.0081.
Toussaint, G. T. (2005) ‘The Euclidean Algorithm Generates Traditional Musical Rhythms’, Bridges: Mathematical Connections in Art, Music, and Science, Banff, Alberta, Canada, 31 July - 3 August.
Toussaint, G. T. (2013) The Geometry of Musical Rhythm. 1 edition. Boca Raton, FL: Routledge.