algoRhythm
algoRhythm is a live music performance where algorithms are used to construct the complexity of polyrhythms. In a sense, it is also a presentation of both the algorithms in rhythmic form and the rhythms in algorithmic form, hence the title. This performance demonstrates the capabilities of a software application developed by me for the purpose of algorithmic music-making.
produced by: Adam He
Introduction
For my artistic practice in algorithmic composition, I have tried using different programming languages to generate musical materials. While most of them have been maturely developed, I still feel that they can not be entirely aligned with my creative process of conception and realisation of rhythm. Therefore, in this work I have invented an experimental programming language that is highly customised to suit my personal needs in algorithmic composition. Also, I have developed an IDE-like software sequencer for encoding and decoding algorithms written in this language. The language and the software sequencer, named PZ as a whole, has been used to create algoRhythm, a demonstrative live music performance.
Concept and background
Musical rhythm is about the organisation of sonic events distributed in time. Its fascination rest upon the arousal of pattern recognition in temporal experience. When it comes to computer-aided algorithmic composition, musicians programme their algorithms to construct and transform patterns over time. Full-fledged musical programming languages like SuperCollider or Max/MSP afford advanced functions to create highly sophisticated patterns. However, the codes or patches written in these languages can become hard to read and interpret for humans - it is to the opposite of intuition which is of great importance in music-making. Therefore, there have been some high-level languages such as ixi lang and TidalCycles developed to facilitate the workflow of composition. These high-level languages pre-build different bespoke frameworks for composition, making them intuitive and handy tools for music-programming. Yet, they are designed to be idiosyncratic, which means a musician’s anatomy of pattern has to agree with the language’s configuration in order for it to be useful. Unfortunately, I happen to be an artist of another kind, who finds no tool out there that can work well with my personal thinking of rhythm, hence deciding to craft my tools. Similar to ixi lang built on SuperCollider and TidalCycles embedded in Haskell, I have devised my high-level language PZ based on Max/MSP.
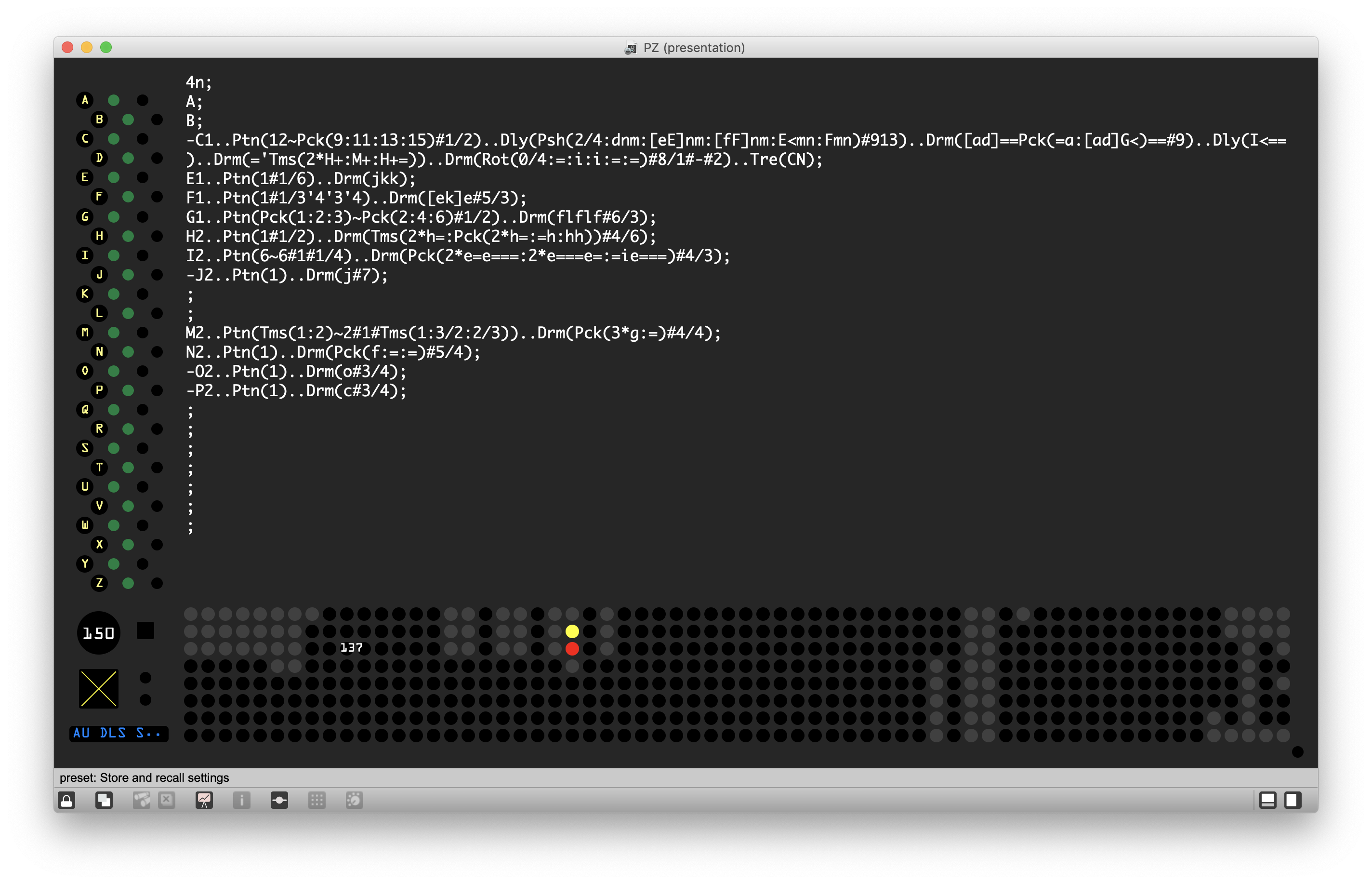
Figure 1 - The user interface of PZ, which consists of a text editor, phrase action indicator, scene navigator, alongside a few global settings and control components.
Architecture - network of phrases
PZ has its own architecture specifically designed to match my methods of organising sonic patterns. Throughout my past practice of algorithmic composition, one of the core techniques that I often use for creating a whole coherent piece is to link fragmental phrases together algorithmically. It is not a unique technique though, I have not yet found any other programming language adopting this generative method at an infrastructural level. The way PZ connects phrases together is fairly straight forward - it affords twenty-six phrase slots per scene, each phrase then is represented by a capital letter ranging from A to Z. To trigger the phrases, one can simply hit A to Z on the computer keyboard of course, but the musical fascination often comes from the algorithmic chain reaction between them. By putting letters A to Z into the definitions of phrase A to Z, they are connected forming an interactional network that is capable of generating well-organised and sophisticated outcome.
A..Ptn(16~16)..Drm(aBa=)..Tre(TmsA:B));
B..Ptn(4~6#1/2)..Drm(=b=bc)..Tre(Tms(C:-:-));
C..Ptn(4~4)..Drm(d==A);
Example 1 - Three connected phrases that can trigger each other along the way they trigger drum sounds.
Metrics - how time is split and added up
PZ affords flexible ways of splitting time by deploying a series of time points based on the multiplication and division of a pulse being the operational unit of time. A pulse is a quarter note by default but can be set to an arbitrary length. For instance, “2/3” is used in PZ to set the pulse as two-third of a quarter note which is handy when mixing two patterns together to create polyrhythms. You can even set it as something like 19/17 to create contra-metrical beats if you want to experiment so. Based on the pulse, a sequence of time point can be arranged. For example, “2’5’2’3” positions four points whose intervals are two, five, two and three pulses respectively. On top of that, if you edit it as “10/2’5’2’3”, it specifies the four points are deployed proportionally over a span of ten pulses, rather than twelve in “2’5’2’3”. This way PZ is compressing or stretching a pattern elastically. Additionally, expressions like “3[2/3’4]1[1/2]” are also accepted as combinations of different metrical grids.
A..Ptn(20#[4/2’3]2#1/2]..Drm(a);
Example 2 - A phrase using an eighth note as a pulse, deploying four time points in a micro period of six pulses repeatedly filling up the whole span of twenty pulses.
Patterning - to blend things up
A percussive sound has at least three attributes, which when to trigger the sound, what sound to be triggered and how hard it is triggered. In the following example “Ptn(9#1’3’2’3)..Drm(ab#937)”, the metrical grid places four time points over a span of nine pulses, drum sounds “a” and “b” are to be triggered successively at these four time points at different velocities “9”, “3” and “7” one by one. The resulted pattern is “1a9, 3b3, 2a7, 3b9”. This principle of patterning is borrowed from SuperCollider, but coupled with much more concise and readable syntax hence higher usability.
A..Ptn(18#1’3’2’1’2)..Drm(ab=b#957#0’127~10);
Example 3 - In addition to the three essential attributes of a percussive sound, PZ can also pattern MIDI control messages. Here “0’127~10” makes a simple pattern of stereo panning, message “0, 127” means “pan to the most left, pan to the most right”.
Sequencing - not only one after another
The function Ptn not only sets metrical grids as above-exemplified, it also controls the way the playhead runs through it. To give an example, Ptn(10~4~2) tells the playhead to start from the third time point (numbered from zero), run four of them repeatedly, and stop after it has reached the ten. Such behaviour generates variations from a single metrical grid in a controllable manner, and is very powerful for rhythmic transformation.
A..Ptn(Tms(10:12:15)~Tms(4:3)~Tms(0:2:4:6:8)#1#1/4)..Drm(a=ab)..Tre(A);
Example 4 - Different variations of playhead behaviour are combined together to create ever-changing transformation of rhythms.
Randomness - surprises keep music alive
There are a few functions to introduce randomness in PZ. For example, Pck picks an item from a list, Shf shuffles items in a list, Dic assigns a variable different values based on probability. There is also a shorthand to produce random integers. For instance, “2/3” returns an integer ranging from 2 to 5, and “4/2/3” multiplies 4 by an integer ranging from 2 to 5. When used as an argument inside a function, it is very handy to quickly generate variations in a continuous space. For example, in Rot(0/3:a=:ab:===:cc:ac), five items “a=”, “ab”, “===”, “cc” and “ac” are forming a list that is to be rotated by a number ranging from 0 to 3, randomly outputting one of the four variations, which may be “a=ab===ccac”, “ab===ccaca=”, “===ccaca=ab” or “ccaca=ab===”.
A..Ptn(2/4/4~6/3~2/0/5#2/3)..Drm(Pck(3*Shf(a:b=:c):Mul(2/4:Rot(0/5:a:=b:d))));
Example 5 - A phrase using controllable randomness to produce many variations from few simple patterns.
Masking - sculpture is about removing the unwanted
Polyrhythm is made not just by cramming different rhythms into one another, very often a sound of a rhythm needs to be muted in order to give room to another sound of another rhythm. Such a technique can produce interlocked patterns similar to those of African polyrhythms. PZ use functions Dly and Drm to layer up patterns. Sounds of lower layers are to be overridden by upper layers. For example, “Dly(a)..Drm(b===)” can produce “baaa”, because “b===” is the upper layer and only when there is no sound (notated as a “=”) can the sound “a” from the lower layer remain. One can also layer an active rest on top of a sound to replace it with silence rather than another sound. For instance, "Dly(a)..Drm(x==x=)" gives "=aa=a", wherein "x" is an active rest and "=" is a passive rest, so "x" mutes the "a" but "=" passes it.
A..Ptn(10)..Dly(ac)..Dly(g==)..Drm(=kk=====)..Drm(i===);
Example 6 - Multiple layers make more complex results. This phase outputs “[ig], k, k, g, [ia], c, g, c, [ia], k”.
Future development
There are much more other details of PZ that are beyond the scope of this essay. In fact, if I intended to developed PZ as a language to be published, I should write a comprehensive user manual. But for now I am happy to keep it to myself for personal usage. I would like to add into it more useful features, such as a function to scatter notes over different time points according to a definable probability distribution, or a function to define continuous curves in which MIDI control messages are to be output. There are too many ideas that can not be elaborated here, but one thing I should always keep in mind would be “less is more”. A high-level language should aim at making users do less to generate more.
Self-evaluation
Overall, I have been happy with what I have made in this project. I studied a wide range of topics including algorithmic composition, rhythm theories, programming languages and HCI design, and then developed a self-sufficient working system that is fully functional to generate a whole piece of live performance demonstrating the capability of constructing highly complex polyrhythms that are difficult or time-consuming to create if solely with its base platform Max/MSP. Along the way, I gained a deeper understanding of the interwoven relations between algorithm, music, notation, instrument, procedural language, creative workflow, and many more.
References
Alex McLean editor and R. T Dean author (2018) The Oxford handbook of algorithmic music. New York, NY: Oxford University Press (Oxford handbooks).
Arom, S. (2004) African polyphony and polyrhythm: musical structure and methodology. Cambridge: Cambridge University Press.
Boenn, G. (2018) Computational models of rhythm and meter. New York, NY: Springer Berlin Heidelberg.
Butler, M. J. (2006) Unlocking the Groove: Rhythm, Meter, and Musical Design in Electronic Dance Music. Pap/Cdr edition. Bloomington: Indiana University Press.
Clayton, M. (2008) Time in Indian music: rhythm, metre, and form in North Indian rāg performance. New York: Oxford University Press (Oxford monographs on music).
-- ixi lang -- (no date). Available at: http://www.ixi-audio.net/ixilang/ (Accessed: 25 August 2019).
Nierhaus, G. (2008) Algorithmic composition: paradigms of automated music generation. Springer Verlag.
SuperCollider » SuperCollider (no date). Available at: https://supercollider.github.io/ (Accessed: 25 August 2019).
TidalCycles userbase (no date). Available at: https://tidalcycles.org/index.php/Welcome (Accessed: 25 August 2019).
Wilson, S., Collins, N. and Cottle, D. (eds) (2011) The SuperCollider book. Cambridge, Mass: MIT Press.